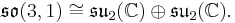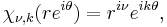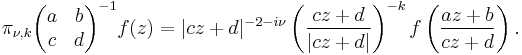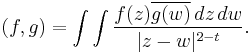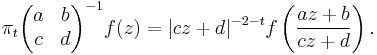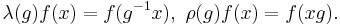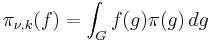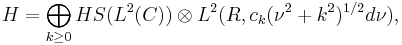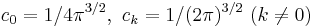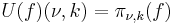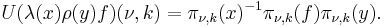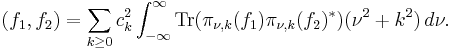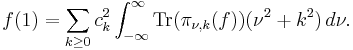Representation theory of the Lorentz group
| Lie groups |
|---|
|
General linear group GL(n)
Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n) |
|
Lie groups in Physics
Particle physics and representation theory
Representation theory of the Lorentz group Representation theory of the Poincaré group Representation theory of the Galilean group |
The Lorentz group of theoretical physics has a variety of representations, corresponding to particles with integer and half-integer spins in quantum field theory. These representations are normally constructed out of spinors.
The group may also be represented in terms of a set of functions defined on the Riemann sphere. these are the Riemann P-functions, which are expressible as hypergeometric functions. An important special case is the subgroup SO(3), where these reduce to the spherical harmonics, and find practical application in the theory of atomic spectra.
The Lorentz group has no unitary representation of finite dimension, except for the trivial representation (where every group element is represented by 1).
Contents |
Finding representations
According to general representation theory of Lie groups, one first looks for the representations of the complexification of the Lie algebra of the Lorentz group. A convenient basis for the Lie algebra of the Lorentz group is given by the three generators of rotations Jk=εijkLij and the three generators of boosts Ki=L0i where i, j, and k run over the three spatial coordinates and ε is the Levi-Civita symbol for a three dimensional spatial slice of Minkowski space. Note that the three generators of rotations transform like components of a pseudovector J and the three generators of boosts transform like components of a vector K under the adjoint action of the spatial rotation subgroup.
This motivates the following construction: first complexify, and then change basis to the components of A = (J + i K)/2 and B = (J – i K)/2. In this basis, one checks that the components of A and B satisfy separately the commutation relations of the Lie algebra su2 and moreover that they commute with each other. In other words, one has the isomorphism
The utility of this isomorphism comes from the fact that su2 is the complexification of the rotation algebra, and so its irreducible representations correspond to the well-known representations of the spatial rotation group; for each j in ½Z, one has the (2j+1)-dimensional spin-j representation spanned by the spherical harmonics with j as the highest weight. Thus the finite dimensional irreducible representations of the Lorentz group are simply given by an ordered pair of half-integers (m,n) which fix representations of the subalgebra spanned by the components of A and B respectively.
Properties of the (m,n) irrep
Since the angular momentum operator is given by J = A + B, the highest weight of the rotation subrepresentation will be m+n. So for example, the (1/2,1/2) representation has spin 1. The (m,n) representation is (2m+1)(2n+1)-dimensional.
Common representations
- (0,0) the Lorentz scalar representation. This representation is carried by relativistic scalar field theories.
- (1/2,0) is the left-handed Weyl spinor and (0,1/2) is the right-handed Weyl spinor representation.
- (1/2,0) ⊕ (0,1/2) is the bispinor representation (see also Dirac spinor).
- (1/2,1/2) is the four-vector representation. The electromagnetic vector potential lives in this rep. It is a 1-form field.
- (1,0) is the self-dual 2-form field representation and (0,1) is the anti-self-dual 2-form field representation.
- (1,0) ⊕ (0,1) is the representation of a parity invariant 2-form field. The electromagnetic field tensor transforms under this representation.
- (1,1/2) ⊕ (1/2,1) is the Rarita-Schwinger field representation.
- (1,1) is the spin-2 representation of the traceless metric tensor.
Full Lorentz group
The (m,n) representation is irreducible under the restricted Lorentz group (the identity component of the Lorentz group). When one considers the full Lorentz group, which is generated by the restricted Lorentz group along with time and parity reversal, not only is this not an irreducible representation, it is not a representation at all, unless m=n. The reason is that this representation is formed in terms of the sum of a vector and a pseudovector, and a parity reversal changes the sign of one, but not the other. The upshot is that a vector in the (m,n) representation is carried into the (n,m) representation by a parity reversal. Thus (m,n)⊕(n,m) gives an irrep of the full Lorentz group. When constructing theories such as QED which is invariant under parity reversal, Dirac spinors may be used, while theories that do not, such as the electroweak force, must be formulated in terms of Weyl spinors.
Infinite dimensional unitary representations
History
The Lorentz group SO(3,1) and its double cover SL(2,C) also have infinite dimensional unitary representations, first studied independently by Bargmann (1947), Gelfand & Naimark (1947) and Harish-Chandra (1947) (at the instigation of Paul Dirac). The Plancherel formula for these groups was first obtained by Gelfand and Naimark through involved calculations. The treatment was subsequently considerably simplified by Harish-Chandra (1951) and Gelfand & Graev (1953), based on an analogue for SL(2,C) of the integration formula of Hermann Weyl for compact Lie groups. Elementary accounts of this approach can be found in Rühl (1970) and Knapp (2001).
The theory of spherical functions for the Lorentz group, required for harmonic analysis on the 3-dimensional hyperboloid in Minkowski space, or equivalently 3-dimensional hyperbolic space, is considerably easier than the general theory. It only involves representations from the spherical principal series and can be treated directly, because in radial coordinates the Laplacian on the hyperboloid is equivalent to the Laplacian on R. This theory is discussed in Takahashi (1963), Helgason (1968), Helgason (2000) and the posthumous text of Jorgenson & Lang (2008).
Principal series
The principal series, or unitary principal series, are the unitary representations induced from the one-dimensional representations of the lower triangular subgroup B of G = SL(2,C). Since the one-dimensional representations of B correspond to the representations of the diagonal matrices, with non-zero complex entries z and z−1, and thus have the form
for k an integer and ν real. The representations are irreducible; the only repetitions occur when k is replaced by –k. By definition the representations are realised on L2 sections of line bundles on G / B = S2, the Riemann sphere. When k = 0, these representations constitute the so-called spherical principal series.
The restriction of a principal series to the maximal compact subgroup K = SU(2) of G can also be realised as an induced representation of K using the identification G / B = K / T, where T = B  K is the maximal torus in K consisting of diagonal matrices with |z|=1. It is the representation induced from the 1—dimensional representation zk T, and is independent of ν. By Frobenius reciprocity, on K they decompose as a direct sum of the irreducible representations of K with dimensions |k| + 2m +1 with m a non-negative integer.
K is the maximal torus in K consisting of diagonal matrices with |z|=1. It is the representation induced from the 1—dimensional representation zk T, and is independent of ν. By Frobenius reciprocity, on K they decompose as a direct sum of the irreducible representations of K with dimensions |k| + 2m +1 with m a non-negative integer.
Using the identification between the Riemann sphere minus a point and C, the principal series can be defined directly on L2(C) by the formula
Irreducibility can be checked in a variety of ways:
- The representation is already irreducible on B. This can be seen directly, but is also a special case of general results on ireducibility of induced representations due to François Bruhat and George Mackey, relying on the Bruhat decomposition G = B
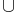 B s B where s is the Weyl group element
B s B where s is the Weyl group element 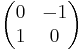 .[1]
.[1]
- The action of the Lie algebra
 of G can be computed on the algebraic direct sum of the irreducible subspaces of K can be computed explicitly and the it can be verified directly that the lowest dimensional subspace generates this direct sum as a
of G can be computed on the algebraic direct sum of the irreducible subspaces of K can be computed explicitly and the it can be verified directly that the lowest dimensional subspace generates this direct sum as a  -module.[2][3]
-module.[2][3]
Complementary series
The for 0 < t < 2, the complementary series is defined on L2 functions f on C for the inner product
with the action given by
The complementary series are irreducible and inequivalent. As a representation of K, each is isomorphic to the Hilbert space direct sum of all the odd dimensional irreducible representations of K = SU(2). Irreducibility can be proved by analysing the action of  on the algebraic sum of these subspaces[2][3] or directly without using the Lie algebra.[4][5]
on the algebraic sum of these subspaces[2][3] or directly without using the Lie algebra.[4][5]
Plancherel theorem
The only irreducible unitary representations of SL(2,C) are the principal series, the complementary series and the trivial representation. Since –I acts ( –1)k on the principal series and trivially on the remainder, these will give all the irreducible unitary representations of the Lorentz group, provided k is taken to be even.
To decompose the left regular representation of G on L2(G), only the principal series are required. This immediately yields the decomposition on the subrepresentations L2(G/ ±I), the left regular representation of the Lorentz group, and L2(G / K), the regular representation on 3-dimensional hyperbolic space. (The former only involves principal series representations with k even and the latter only those with k = 0.)
The left and right regular representation λ and ρ are defined on L2(G) by
Now if f is an element of Cc(G), the operator π\nu,k (f) defined by
is Hilbert-Schmidt. We define a Hilbert space H by
where
and HS(L2(C)) denotes the Hilbert space of Hilbert-Schmidt operators on L2(C).[6] Then the map U defined on Cc(G) by
extends to a unitary of L2(G) onto H.
The map U satisfies
If f1, f2 are in Cc(G) then
Thus if f = f1  f2* denotes the convolution of f1 and f2*, where
f2* denotes the convolution of f1 and f2*, where 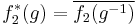 , then
, then
The last two displayed formulas are usually referred to as the Plancherel formula and the Fourier inversion formula respectively. The Plancherel formula extends to all fi in L2(G). By a theorem of Jacques Dixmier and Paul Malliavin, every function f in 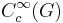 is a finite sum of convolutions of similar functions, the inversion formula holds for such f. It can be extended to much wider classes of functions satisfying mild differentiability conditions.[7]
is a finite sum of convolutions of similar functions, the inversion formula holds for such f. It can be extended to much wider classes of functions satisfying mild differentiability conditions.[7]
See also
Notes
- ^ Knapp 2001, Chapter II
- ^ a b Harish-Chandra 1947
- ^ a b Taylor 1986
- ^ Gelfand & Naimark 1947
- ^ Takahashi 1963, p. 343
- ^ Note that for a Hilbert space H, HS(H) may be identified canonically with the Hilbert space tensor product of H and its conjugate space.
- ^ Knapp 2001
References
- Bargmann, V. (1947), "Irreducible unitary representations of the Lorenz group", Ann. Of Math. 48 (3): 568–640, doi:10.2307/1969129, JSTOR 1969129 (the representation theory of SO(2,1) and SL(2,R); the second part on SO(3,1) and SL(2,C), described in the introduction, was never published).
- Dixmier, J.; Malliavin, P. (1978), "Factorisations de fonctions et de vecteurs indéfiniment différentiables", Bull. Sc. Math. 102: 305–330
- Gelfand, I. M.; Naimark, M. A. (1947), "Unitary representations of the Lorentz group", Izvestiya Akad. Nauk SSSR. Ser. Mat. 11: 411–504
- Gelfand, I. M.; M. I. Graev (1953), Doklady Akademii Nauk SSSR 92: 221–224
- Harish-Chandra (1947), "Infinite irreducible representations of the Lorentz group", Proc. Roy. Soc. London. Ser. A. 189 (1018): 372–401, doi:10.1098/rspa.1947.0047
- Harish-Chandra (1951), "Plancherel formula for complex semi-simple Lie groups", Proc. Nat. Acad. Sci. U. S. A. 37 (12): 813–818, doi:10.1073/pnas.37.12.813
- Helgason, S. (1968), Lie groups and symmetric spaces, Battelle Rencontres, Benjamin, pp. 1–71 (a general introduction for physicists)
- Helgason, S. (2000), Groups and geometric analysis. Integral geometry, invariant differential operators, and spherical functions (corrected reprint of the 1984 original), Mathematical Surveys and Monographs, 83, American Mathematical Society, ISBN 0-8218-2673-5
- Jorgenson, J.; Lang, S. (2008), The heat kernel and theta inversion on SL(2,C), Springer Monographs in Mathematics, Springer, ISBN 978-0-387-38031-5
- Knapp, A. (2001), Representation theory of semisimple groups. An overview based on examples., Princeton Landmarks in Mathematics, Princeton University Press, ISBN 0-691-09089-0 (elementary treatment for SL(2,C))
- Naimark, M.A. (1964), Linear representations of the Lorentz group (translated from the Russian original by Ann Swinfen and O. J. Marstrand), Macmillan
- Paërl, E.R. (1969) Representations of the Lorentz group and projective geometry, Mathematical Centre Tract #25, Amsterdam.
- Rühl, W. (1970), The Lorentz group and harmonic analysis, Benjamin (a detailed account for physicists)
- Takahashi, R. (1963), "Sur les représentations unitaires des groupes de Lorentz généralisés", Bull. Soc. Math. France 91: 289–433
- Taylor, M.E. (1986), Noncommutative harmonic analyis, Mathematical Surveys and Monographs, 22, American Mathematical Society, ISBN 0-8218-1523-7, Chapter 9, SL(2,C) and more general Lorentz groups